Bạn đang xem: Các lệnh cơ bản trong matlab giải tích
phía dẫn áp dụng Mat
Lab trong môn Giải tích Matlab là 1 trong những hệ giám sát lớn cùng mạnh, được dùng phổ cập trong giảng dạy, nghiên cứu và phân tích và làm việc thực tế. Tuy nhiên phần mượt này có phiên bản quyền, kha khá cồng kềnh, có thể lên tới sản phẩm gigabybes Tài liệu phía dẫn đa số là phần Help của chương trình. Dường như có thể tìm hiểu quyển sách Jeffery Cooper, A Matlab companion for multivariable calculus, Harcourt, 2001. Thông tin biến x là một biến kí hiệu (symbolic) syms x Nhập vào hàm f, lấy ví dụ f(x)=x^2-3x+1 f=x^2-3*x+1 Tính quý hiếm của hàm Tính quý hiếm của f tại một điểm, ví dụ điển hình tại x=2 subs(f,x,2) Tính đạo hàm Tính đạo hàm của hàm f theo đổi mới x diff(f,x) Vẽ vật dụng thị hàm một trở nên Vẽ thứ thị hàm f, chẳng hạn với x từ 1 tới 2 ezplot(f,<1,2>) Tích phân của hàm một biến đổi Tính tích phân không xác minh của hàm f theo thay đổi x int(f,x) Tính tích phân khẳng định của hàm f theo phát triển thành x, với x từ là một tới 2 int(f,x,1,2) Nhập hàm nhiều đổi thay ở dạng kí hiệu Nhập vào trong 1 hàm nhiều đổi mới syms x y f=x^2*y^3-3*x*y^2 Tính cực hiếm của hàm hai phát triển thành Tính quý giá của f trên một điểm, ví dụ điển hình tại x=2, y=3 subs(subs(f,x,2),y,3) Tính đạo hàm riêng Tính đạo hàm riêng rẽ của f theo vươn lên là y diff(f,y) Vẽ đồ thị hàm hai phát triển thành Vẽ vật thị hàm f trên khoảng chừng x từ một tới 2, y từ bỏ 3 cho tới 4 ezsurf(f,<1,2,3,4>) Tính tích phân bội Tính tích phân của f bên trên hình vỏ hộp chữ nhật x từ 1 tới 2, y trường đoản cú 3 tới 4: Đưa về tích phân lặp: int(int(f,x,1,2),y,3,4) Vẽ phương diện cho vày phương trình tham số ví dụ vẽ mặt mong x=sin(u)cos(v), y=sin(u)sin(v), z=cos(u), u trường đoản cú 0 cho tới pi, v từ 0 cho tới 2pi: syms u v ezsurf(sin(u)*cos(v),sin(u)*sin(v),cos(u),<0 pi 0 2*pi>) chủng loại lệnh tổng thể là ezsurf(x,y,z,) tham số đầu tiên biến thiên tự a cho tới b, tham số vật dụng hai vươn lên là thiên từ c cho tới d. Tính giao động tích phân Tính dao động tích phân của hàm f (x) cùng với x từ a tới b: bởi đây không thể là phép toán kí hiệu nữa mà là phép toán số (numerical), nên bắt buộc chuyển f thành một dạng hàm khác, call là inline. Lấy một ví dụ tích tích phân f(x)=e^(x^2) trường đoản cú 0 cho tới 1: Nhập hàm f sinh sống dạng inline f=inline('exp(x.^2)') chăm chú có dấu chấm trước toán tử ^ (Matlab dùng nó để giám sát trên ma trận). Tính giao động tính phân của f: quad(f,0,1) Vẽ ngôi trường vectơ 2 chiều Ví dụ: Vẽ trường (P(x,y),Q(x,y)) cùng với P(x,y)=2x+3y, Q(x,y)=3x^2-y^5 bên trên hình chữ nhật x từ -1 cho tới 1, y từ -2 tới 2. Nhập vào trường: P=inline('2*x+3*y','x','y') Q=inline('3*x^2-y^5','x','y') Cho trở nên x chạy từ bỏ -1 tới 1, lấy 10 điểm chia; cho biến y chạy từ bỏ -2 cho tới 2, đem 10 điểm chia: x=linspace(-1,1,10) y=linspace(-2,2,10) chế tạo ra một lưới những điểm ứng với những điểm phân chia trên:
Lab trong môn Giải tích Matlab là một trong những hệ đo lường và thống kê lớn cùng mạnh, được dùng phổ biến trong giảng dạy, nghiên cứu và phân tích và thao tác thực tế. Mặc dù phần mượt này có phiên bản quyền, tương. Tới pi, v từ 0 tới 2pi: syms u v ezsurf(sin(u)*cos(v),sin(u)*sin(v),cos(u),<0 pi 0 2*pi>) mẫu lệnh tổng thể là ezsurf(x,y,z,) tham số trước tiên biến thiên từ bỏ a cho tới b, tham số thứ
1/ MATLAB có thể chấp nhận được ta nhập số liệu từ cái lệnh. Lúc nhập ma trận từ keyboard ta phải tuân theo những quy định sau :
• phân làn các bộ phận của ma trận bởi dấu “,” hay vệt trống
• dùng dấu “;” để dứt một sản phẩm
• bao các phần tử của ma trận bằng cặp lốt ngoặc vuông < >
Ví dụ : >> A = < 1 2 3 > hiệu quả là A = 1 2 3 >> A = <1;2;3>
hiệu quả là A =
1
2 3
2/ Toán tử ‘ dùng để chuyển vị một ma trận thực và chuyển vị phối hợp một ma trận
phức. Ví như chỉ ao ước chuyển vị ma trận phức, ta cần sử dụng thêm toán tử “.” nghĩa là đề nghị
viết “.’”. Ví dụ:
C = <1 + 2*i 2 - 4*i; 3 + i 2 - 2*j>;
X = C"
Y = C.’
3/ Chỉ số: bộ phận ở mặt hàng i cột j của ma trận m×n bao gồm kí hiệu là A(i, j). Mặc dù
nhiên ta cũng hoàn toàn có thể tham chiếu tới phần tử của mảng nhờ vào một chỉ số, lấy một ví dụ A(k) với k
= i + (j - 1)m. Biện pháp này thường dùng để làm tham chiếu vec tơ hàng hay cột. Trong trường
hợp ma trận rất đầy đủ thì nó được coi là ma trận một cột dài tạo từ các cột của ma trận
ban đầu. Bởi vậy viết A(5) tức là tham chiếu bộ phận A(2, 2).
Để xác định kích thước của một ma trận ta sử dụng lệnh length(trả về kích thước
lớn nhất) hay size(số hàng và cột). Ví dụ:
c = <1 2 3 4; 5 6 7 8>;
length(c)
4/ Toán tử “:” : Toán tử “:” là một trong những toán tử quan trọng của MATLAB. Nó xuất
hiện ở những dạng không giống nhau. Ví dụ: Lệnh :
1:10
tạo một vec tơ hàng chứa 10 số nguyên từ là một đến 10.
Lệnh: 100: -7: 50
tạo một hàng số từ 100 mang lại 51, giảm 7 từng lần.
Các biểu thức chỉ số tham chiếu tới 1 phần của ma trận. Viết A(1:k, j) là tham
chiếu cho k phần tửđầu tiên của cột j. Ngoài ra toán tử “:” tham chiếu tới tất cả các
phần tử của một hàng hay là một cột. Ví dụ:
B = A(:, <1 3 2 >)
tạo ra ma trận B tự ma trận A bằng phương pháp đổi đồ vật tự các cột từ <1 2 3> thành <1 3 2>
Tạo ma trận bởi hàm gồm sẵn: MATLAB hỗ trợ một số hàm nhằm tạo các
ma trận cơ bản:
zeros tạo nên ma trận mà các phần tửđều là zeros
z = zeros(2, 4)
ones tạo nên ma trận mà các phần tửđều là 1
x = ones(2, 3)
y = 5*ones(2, 2)
rand tạo nên ma trận nhưng các phần tử ngẫu nhiên phân bốđều
d = rand(4, 4)
randn tạo ra ma trận mà lại các bộ phận ngẫu nhiên phân bổ trực giao
e = randn(3, 3)
magic(n) tạo thành ma trận cấp cho n gồm các số nguyên từ là 1 đến n2 cùng với tổng các hàng
bằng tổng các cột (n phải lớn hơn hay bằng 3).
pascal(n) tạo ra ma trận xác minh dương cấp cho n nhưng các thành phần lấy từ tam giác Pascal.
Lệnh :
pascal(4) tạo thành ma trận xác định dương cấp 4
- eye(n) sinh sản ma trận đơn vị chức năng cấp n
Lệnh:
eye(3) tạo ma trận đơn vị chức năng cấp 3
- eye(m, n) chế tác ma trận 1-1 vị mở rộng
Lệnh:
eye(3, 4) chế tạo ra ma trận đơn vị chức năng gồm 3 mặt hàng 4 cột
Ta hoàn toàn có thể lắp ghép(concatenation) những ma trận có sẵn thành một
ma trận mới. Ví dụ:
a = ones(3, 3)
b = 5*ones(3, 3)
Xoá hàng với cột : Ta có thể xoá hàng với cột tự ma trận bằng dùng vết <>. Để
xoá cột thứ 2 của ma trận b ta viết:
b(:, 2) = <>
Các lệnh xử lý ma trận:
cộng : X= A + B
Trừ : X= A - B
Nhân : X= A * B
: X.*A nhân các bộ phận tương ứng với nhau
phân chia : X = A/B lúc đó X*B = A
: X = AB dịp đó A*X = B
: X=A./B phân tách các thành phần tương ứng với nhau
Luỹ vượt : X = A^2
: X = A.^2
Nghịch hòn đảo : X = inv(A)
Định thức : d = det(A)
Số chiều của mình vector A : n=ndims(A)
Tổng các phần tử trên đường chéo chính ma trận A : s = trace(A)
Phần 2.
Yêu cầu: Sinh viên không được dùng những hàm sẵn tất cả trong matlab nhằm viết chương trình.
Các đề tài.
1/ Dùng các phép thay đổi sơ cấp đưa ma trận về dạng bậc thang và kiếm tìm hạng của ma trận A tùy ý.
Yêu cầu: Input: được cho phép nhập vào một ma trận tùy ý. Output: Ma trận bậc thang và r(A).
2/ Nhân nhị ma trận với nhau.
Yêu cầu: Input: có thể chấp nhận được nhập vào nhị ma trận A và B. Chương trình bắt buộc kiểm tra phép nhân có tiến hành được hay không? Output: Ma trận tích.
3/ Tính Am, cùng với m là số tự nhiên cho trước.
Yêu cầu: Input: Nhập vào một trong những ma trận vuông tùy ý cùng số tự nhiên m. Output: một ma trận Am.
4/ Tính định thức của ma trận bằng chuyển đổi sơ cấp.
Yêu cầu: Input: được cho phép nhập vào một trong những ma trận vuông tùy ý. Output: det(A).
5/ Tính định thức của ma trận vuông A bằng phương pháp khai triển theo một mặt hàng tùy ý (hoặc một cột tùy ý) qua các bù đại số.
Yêu cầu: Input: chất nhận được nhập vào trong 1 ma trận vuông tùy ý. Output: det(A).
6/ kiếm tìm hạng của ma trận bằng những sử dụng các định thức bé (phương pháp định thức bao quanh).
7/ tìm ma trận nghịch hòn đảo của ma trận vuông A bằng biến đổi sơ cấp đối với hàng cho ma trận
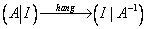
Yêu cầu: Input: cho phép nhập vào một ma trận vuông tùy ý. Chương trình kiểm tra tính khả nghịch của ma trận. Output: Ma trận nghịch đảo: .
8/ tìm ma trận nghịch hòn đảo bằng cách làm
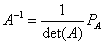
Yêu cầu: Input: chất nhận được nhập vào trong 1 ma trận vuông tùy ý. Chương trình soát sổ tính khả nghịch của ma trận. Output: Ma trận nghịch đảo: .
9/ so sánh LU của ma trận A. Phân tích PA=LU.
Yêu cầu: Input: chất nhận được nhập vào một ma trận vuông cung cấp n. Chương trình chất vấn A rất có thể phân tích thành A = LU tuyệt không. Còn nếu không thì tra cứu ma trận p. Và phân tích PA= LU. Output: Ma trận nghịch đảo: P, L, U.
11/ kiểm soát tính khẳng định dương của ma trận vuông A. (định nghĩa: ma trận vuông A call là xác định dương, nếu các định thức con chủ yếu đều dương).
10/ so với Cholesky:
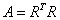
11/ Giải hệ phương trình bằng phép biến đổi Gauss.
Yêu cầu: Input: có thể chấp nhận được nhập vào một ma trận tùy ý A cùng ma trận b. Output: Nghiệm của hệ sống dạng vécto.
Ma trận A và b có thể được đọc từ file *.txt
12/ Giải hệ Cramer AX = b với A vuông,
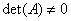
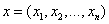
trong đó
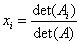
13/ tìm kiếm tọa độ của một vécto vào một đại lý cho trước.
Yêu cầu: Input: cho một vécto với một đại lý E. Output: tọa độ của vécto trong đại lý E.
14/ tra cứu ma trận chuyển các đại lý từ E sang trọng F.
Yêu cầu: Input: cho hai cơ sở E với F. Output: ma trận chuyển cơ sở phường
15/ tìm kiếm hạng của mình vécto.
Yêu cầu: Input: cho một họ vécto. Output: hạng của mình vécto này và những vécto hòa bình tuyến tính buổi tối đa của mình
16/ chất vấn tính chủ quyền tuyến tính, phụ thuộc tuyến tính của họ vécto. Khám nghiệm vécto x có là tổng hợp tuyến tính của họ vécto M hay không?
17/ search cơ sở, số chiều của không gian con sinh ra bởi vì họ vécto M.
Yêu cầu: Input: cho phép nhập vào trong 1 họ vécto. Output: Số chiều và cửa hàng của không gian con sinh ra vì M.
18/ Tìm các đại lý và số chiều của không gian nghiệm của hệ thuần độc nhất AX = 0.
Yêu cầu: Input: chất nhận được nhập vào ma trận A. Output: Số chiều và các đại lý của không gian nghiệm.
19/ tìm số chiều và cửa hàng của không gian giao
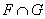
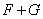
20/ Dùng quá trình trực giao hóa Gram-Schmidt, tìm bọn họ trực giao, bọn họ trực chuẩn của họ vécto độc lập tuyến tính.
Yêu cầu: Input: cho phép nhập vào một trong những họ vécto bao gồm m vécto hòa bình tuyến tính (hoặc họ vécto bất kỳ, chương trình yêu cầu kiểm tra tính độc lập tuyến tính của họ vécto). Output: Họ bao gồm m vécto trực giao, rất có thể trực chuẩn.
21/ phân tích QR của ma trận vuông A bằng quy trình Gram – Schmidt.
Yêu cầu: Input: có thể chấp nhận được nhập vào ma trận vuông A tùy ý. Chương trình soát sổ A có phân tích QR hay là không (điều kiện: các cột của A là họ hòa bình tuyến tính). Output: Ma trận Q và ma trận R.
22/ search hình chiếu vuông góc của một vécto cho trước xuống không gian con. Tìm khoảng cách từ vécto đến không khí con.
Yêu cầu: Input: có thể chấp nhận được nhập vào một trong những họ vécto M và vécto x. Output: hình chiếu vuông góc của vecto x xuống không gian con F được sinh ra vị M và khoảng cách từ x cho F.
23/ mang đến ánh xạ tuyến tính f biết ma trận của f trong cơ sở E là A. Tìm ảnh của một vécto đến trước.
24/ cho ánh xạ đường tính f biết ma trận của f trong các đại lý E là A. Search cơ sở, số chiều của nhân và hình ảnh của ánh xạ tuyến tinh.
25/ cho ánh xạ đường tính f. Kiếm tìm ma trận của ánh xạ tuyến đường tính trong các đại lý E mang lại trước.
26/ cho ma trận vuông A. Tra cứu trị riêng, vécto riêng biệt của ma trận A.
27/ đến ma trận vuông A. Khám nghiệm tính chéo hóa của A. Giả dụ được, tra cứu ma trận p và ma trận D.
28/ đến ma trận đối xứng, thực vuông A. Chéo hóa trực giao ma trận A.
29/ đến ma trận vuông A chéo cánh hóa được. Tính Am.
30/ mang lại dạng toàn phương . Soát sổ dạng toàn phương khẳng định dương giỏi không.
31/ mang lại dạng toàn phương . Đưa dạng toàn phương về chính tắc bằng thay đổi trực giao.
32/ đến dạng toàn phương . Phân các loại dạng toàn phương.
33/ Ứng dụng ma trận nghịch hòn đảo trong định hướng mật mã
34/ Ứng dụng đại số con đường tính trong việc xấp xĩ hàm.
35/ Ứng dụng đại số con đường tính trong kim chỉ nan đồ họa.
Phần 3. Các chương trình tham khảo. Những chương trình này được download từ mạng hoặc nhiều phần do sv viết buộc phải chưa chắc là về tối ưu.
1/ dùng thay đổi sơ cấp đưa ma trận về dạng lan can
function A=bdsc_bacthang(B)
A=B;
h=1;
for k=1:m-1;
for j=h:n;
for i=k:m;
if(A(i,j)~=0)
break;
end;
end;
if(A(i,j)~=0)
break;
end;
end;
if(i~=k)
for l=h:n;
a=A(k,l);
A(k,l)=A(i,l);
A(i,l)=a;
end;
end;
if(j~=h)
h=j;
end;
for i=k+1:m;
if (A(i,h)~=0)
a=A(i,h)/A(k,h);
for j=h:n;
A(i,j)=A(i,j)-a*A(k,j);
end;
end;
end;
h=h+1;
end;
disp("ma tran bac thang");
disp(A);
end
1b/ dùng đổi khác sơ cấp đem về dạng bậc thang, tính hạng cùng tính định thức.
function
% Dong thoi tim dinh thuc va hang cua ma tran dua vao bdsc
if nargin "phai nhap vao ma tran can phan tich");
end;
N = size(A,1);%1 la dong,2 la cot,i la hang,j la cot
m = size(A,2);
l=A;
i=1;
d=0;
if N~=m
dinhthuc ="*phai la ma tran vuong*";
end;
for h=1:N
k=l(h:N,:);
k=k(:,h:m);
for j=1:(m-h+1) % tim phan tu khac khong dau tien theo tt cot hang
for i=1:(N-h+1)
if k(i,j)~=0
e=i;
if h==1
f=j;
end;
if h~=1
f=1;
end;
break;
end;
end;
if k(i,j)~=0
break;
end;
end;
d=d+(e-1)*(N-1)+(f-1)*(m-1);
k=circshift(k, <-(e-1), -(f-1)>);
p=
l=
for g=h:(N-1) % quần thể cac phan tu theo sau ben duoi
for i=(g+1):N
if l(g,g)~=0
c=l(i,g)/l(g,g);
for j=g:m
l(i,j)=l(i,j)-(c*l(g,j));
end;
end;
if l(g,g)==0
break;
end;
end;
if l(g,g)==0
break;
end;
end;
end;
E=l(2:N,1:m,:); % bien doi de dinh thuc ma tran khong cố kỉnh doi
F=l(1,1:m);
F=((-1)^d)*F;
B=
hang=0;
for s=1:N %tim hang ma tran
i=N+1-s;
for j=1:m
if B(i,j)~=0
hang=i;
break;
end;
end;
if B(i,j)~=0
break;
end;
end;
if N==m % tim dinh thuc ma tran
dinhthuc=1;
for i=1:N
dinhthuc=dinhthuc*B(i,i);
end;
end;
2/ Giải hệ phương trình bằng phương pháp Cramer
function
if nargin "phai nhap vao ma tran can phan tich");
end;
N = size(A,1);%1 la dong,2 la cot,i la hang,j la cot
m = size(A,2);
if N~=m error ("khong phai la he cramer,nhap lai ma tran he so A");
end;
n = size(b,1);
M = size(b,2);
if n>M
b=b";
if M~=1 error ("kich co he so tu vày khong phu hop nhap lai b");
end;
if n~=N error ("kich co he so tu vày khong phu hop nhap lai b");
end;
end;
if M>n
if n~=1 error ("kich teo he so tu vị khong phu hop nhap lai b");
end;
if M~=N error ("kich co he so tu vì khong phu hop nhap lai b");
end;
end;
if det(A)==0 error ("det=0,khong the dung phuong phap nay");
end;
l=A;
X=0;
b=b";
for j=1:N
if j==1
l=A;
l(:,j)=<>;
l=;
X(1,j)=det(l)/det(A);
end;
if j>=2
if j
l=A;
a=l;
x=a(1:N,1:(j-1),:);
y=a(1:N,(j+1):N,:);
l=
l=
X(1,j)=det(l)/det(A);
end;
if j==N
l=A;
l(:,j)=<>;
l=
X(1,j)=det(l)/det(A);
end;
end;
end;
3/ Giải hệ bằng cách thức khử Gauss
function
if nargin "phai nhap vao ma tran can phan tich");
end;
N = size(A,1);%1 la dong,2 la cot,i la hang,j la cot
m = size(A,2)+1;
z = size(b,1);%kiem tra he so tu bởi vì
t = size(b,2);
c=b;
if t>z
for j=1:t % chuyen vi ma tran
for i=1:z
b(j,i)=c(i,j);
end;
end;
b=b(:,1:z);
end;
if z>t
b=c;
end;
z = size(b,1);
t = size(b,2);
%if z~=1
% if t==N error ("kich co he so tu bởi vì khong phu hop");
% end;
%end;
%if t~=1 error ("kich teo he so tu vị khong phu hop.");
%end;
l=;
i=1;
d=0;
for h=1:N
k=l(h:N,:);%chon hang thu h den N
k=k(:,h:m); %chon cot thu h den m
for j=1:(m-h+1)
for i=1:(N-h+1)
if k(i,j)~=0
e=i;
if h==1
f=j;
end;
if h~=1
f=1;
end;
break;
end;
end;
if k(i,j)~=0
break;
end;
end;%tim phan tu khac 0 dau tien de hoan doi
k=circshift(k, <-(e-1), -(f-1)>);
p=
l=
for g=h:(N-1)
for i=(g+1):N
if l(g,g)~=0
c=l(i,g)/l(g,g);
for j=g:m
l(i,j)=l(i,j)-(c*l(g,j));
end;
end;
if l(g,g)==0
break;
end;
end;
if l(g,g)==0
break;
end;
end;% bien doi so cap khu cac phan tu ben duoi
end;
B=l;
r
A=0;
r
B=0;
for s=1:N
i=N+1-s;
for j=1:(m-1)
if B(i,j)~=0
r
A=i;
break;
end;
end;
if B(i,j)~=0
break;
end;
end;%tim hang ma tran he so
for s=1:N
i=N+1-s;
for j=1:m
if B(i,j)~=0
r
B=i;
break;
end;
end;
if B(i,j)~=0
break;
end;
end;% tim hang ma tran mo rong
if r
A
X= ("phuong trinh vo nghiem");
end;
if r
A==r
B
if r
Xem thêm: Khám Phá Top Khách Sạn Tam Đảo Giá Rẻ Đẹp Đáng Cho Du Khách Lưu Trú
A
X= ("phuong trinh co vo so nghiem");
end;
u=0;
if r
A==(m-1) %giai nghiem he theo phuong phap quần thể Gauss
for s=1:(m-1)
i=m-s;
if i==(m-1);
X(i)=B(i,m)/B(i,i);
end;
if i~=(m-1)
for c=1:(s-1)
y=m-c;
u=u+X(y)*B(i,y);
X(i)=(B(i,m)-u)/B(i,i);
end;
end;
u=0;
end;
end;
end;
4/ tìm ma trận nghịch đảo
function = nghichdao (A)% tim ma tran nghich dao theo ma tran phu hop
if nargin "phai nhap vao ma tran can phan tich");
end;
N = size(A,1);%1 la dong,2 la cot,i la hang,j la cot
m = size(A,2);
d=0;
a=A;
i=1;
if N~=m
error ("ma tran khong vuong");
end;
l=A;
for h=1:N %bien doi bac thang
k=A(h:N,:);
k=k(:,h:N);
for j=1:(N-h+1)
for i=1:(N-h+1)
if k(i,j)~=0
e=i;
if h==1
f=j;
end;
if h~=1
f=1;
end;
break;
end;
end;
if k(i,j)~=0
break;
end;
end;
d=d+(e-1)*(N-1)+(f-1)*(N-1);
k=circshift(k, <-(e-1), -(f-1)>);
p=
A=
for g=h:(N-1)
for i=(g+1):N
if A(g,g)~=0
c=A(i,g)/A(g,g);
for j=g:N
A(i,j)=A(i,j)-(c*A(g,j));
end;
end;
if A(g,g)==0
break;
end;
end;
if A(g,g)==0
break;
end;
end;
end;
E=A(2:N,1:N,:);
F=A(1,1:N);
F=((-1)^d)*F;
K=
dinhthuccha=1;
for i=1:N %tinh dinh thuc
dinhthuccha=dinhthuccha*K(i,i);
end;
for o=1:N
l(o,:)=<>;
D=l;
for t=1:N
l(:,t)=<>;
N=N-1;
for h=1:N
k=l(h:N,:);
k=k(:,h:N);
for j=1:(N-h+1)
for i=1:(N-h+1)
if k(i,j)~=0
e=i;
if h==1
f=j;
end;
if h~=1
f=1;
end;
break;
end;
end;
if k(i,j)~=0
break;
end;
end;
d=d+(e-1)*(N-1)+(f-1)*(N-1);
k=circshift(k, <-(e-1), -(f-1)>);
p=
l=
for g=h:(N-1)
for i=(g+1):N
if l(g,g)~=0
c=l(i,g)/l(g,g);
for j=g:N
l(i,j)=l(i,j)-(c*l(g,j));
end;
end;
if l(g,g)==0
break;
end;
end;
if l(g,g)==0
break;
end;
end;
end;
E=l(2:N,1:N,:);
F=l(1,1:N);
F=((-1)^d)*F;
G=
dinhthuccon=1;
for i=1:N
dinhthuccon=dinhthuccon*G(i,i);
end;
B(o,t)=((-1)^(o+t))*dinhthuccon;
dinhthuccon=1;
l=D;
N=N+1;
end;
l=a;
end;%tim ma tran dinh thuc bé
C=B;
for j=1:N % chuyen vi ma tran
for i=1:N
B(i,j)=C(j,i);
end;
end;
B=B/dinhthuccha;
5/Phân tích LU của ma trận A
function
if nargin "phai nhap vao ma tran can phan tich");
end;
a=A;
N = size(A,1);%1 la dong,2 la cot
m = size(A,2);
if N~=m
A = ("khong la ma tran vuong");
end;
if N==m
l=zeros(N);
u=zeros(N);
for i=1:N
l(i,i)=1;
end;
for j=1:N
u(1,j)=A(1,j);
end;
if u(1,1)== 0
error("khong the phan tich duoc, nhap lai ma tran khac");
end;
for i=2:N
l(i,1)=A(i,1)/u(1,1);
end;
for i=2:N-1
for j=i:N
sum=0;
for k=1:i-1
sum=sum+l(i,k)*u(k,j);
end;
u(i,j)=A(i,j)-sum;
end;
if u(i,i)==0
error("khong the phan tich duoc, nhap lai ma tran khac");
end;
for j=i+1:N
sum=0;
for k=1:i-1
sum=sum+l(j,k)*u(k,i);
end;
l(j,i)=(A(j,i)-sum)/u(i,i);
end;
end;
sum=0;
for k=1:N-1
sum=sum+l(N,k)*u(k,N);
end;
u(N,N)=A(N,N)-sum;
dinhthuc=1;
for i=1:N
dinhthuc = dinhthuc*u(i,i)*l(i,i);
end;
end;
A=a;
6/ Dùng quá trình trực giao Gram-Schmidt đưa họ tự do tuyến tính về bọn họ trực chuẩn
function orthonormal_basis = Gram_Schmidt_process(A)
matrix_size = size(A);
m = matrix_size(1,1);
n = matrix_size(1,2);
if A == zeros(m,n)
error("There does not exist any type of basis for the zero vector space.");
elseif n == 1
orthonormal_basis = A(1:m,1)/norm(A(1:m,1));
else
flag = 0;
if is_orthonormal_set(A) == 1
orthonormal_basis = A;
flag = 1;
kết thúc
if flag == 0;
if rank(A) ~= n
A = basis_col(A);
over
matrix_size = size(A);
m = matrix_size(1,1);
n = matrix_size(1,2);
orthonormal_basis = A(1:m,1)/norm(A(1:m,1));
for i = 2:n
u = A(1:m,i);
v = zeros(m,1);
for j = 1:(i - 1)
v = v - dot(u,orthonormal_basis(1:m,j))*orthonormal_basis(1:m,j);
over
v_ = u + v;
orthonormal_basis(1:m,i) = v_/norm(v_);
kết thúc
end
end
7/ kiểm soát họ vécto liệu có phải là họ trực giao
function result = is_orthogonal_set(A)
matrix_size = size(A);
m = matrix_size(1,1);
n = matrix_size(1,2);
tolerance = 10^-10;
if n == 1
result = 1;
else
orthogonal_counter = 0;
for i = 1:n
for j = 1:n
if i == j
else
if abs(dot(A(1:m,i),A(1:m,j)))
orthogonal_counter = orthogonal_counter + 1;
over
kết thúc
over
end
if orthogonal_counter == factorial(n)/factorial(n - 2);
result = 1;
else
result = 0;
over
end
8/ việc bình phương rất tiểu.
function c = fit(n, t, y)
% The least-squares approximating polynomial of degree n (n>=0).
% Coordinates of points to lớn be fitted are stored in the column vectors
% t & y. Coefficients of the approximating polynomial are stored in
% the vector c. Graphs of the data points and the least-squares
% approximating polynomial are also generated.
if ( n >= length(t))
error("Degree is too big")
end
v = fliplr(vander(t));
v = v(:,1:(n+1));
c = vy;
c = fliplr(c");
x = linspace(min(t),max(t));
w = polyval(c, x);
plot(t,y,"ro",x,w);
title(sprintf("The least-squares polynomial of degree n = %2.0f",n))
legend("data points","fitting polynomial")
Chạy thử công tác trên bằng cách nhập:
a/ t = linspace(0, pi/2, 10); t = t";
b/ y = sin(2*t);
c/ c = fit(3, t, y)
9/ Ứng dụng trong kim chỉ nan mật mã.
Đoạn code dùng mã hóa thông tin
function B = code(s, A)
% String s is coded using a nonsingular matrix A.
% A coded message is stored in the vector B.
p = length(s);
b = double(s);
r = rem(p,n);
if r ~= 0
b = ";
end
b = reshape(b,n,length(b)/n);
B = A*b;
B = B(:)";
Đoạn code lời giải thông tin
function s = dcode(B, A)
% Coded message, stored in the vector B, is
% decoded with the aid of the nonsingular matrix A
% and is stored in the string s.
p = length(B);
B = reshape(B,n,p/n);
d = AB;
s = char(d(:)");
Chạy thử lịch trình trên:
a/ s=’Toi hoc dẻo so tuyen tinh’
b/ A=pascal(4) tạo thành ma trận khả nghịch tùy ý( trong trường đúng theo này cần sử dụng mt pascal cấp 4)